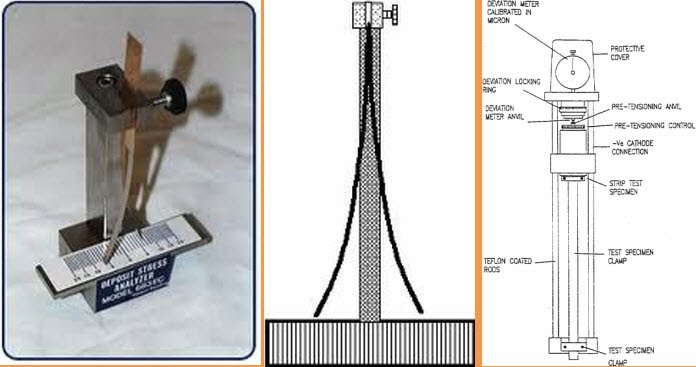
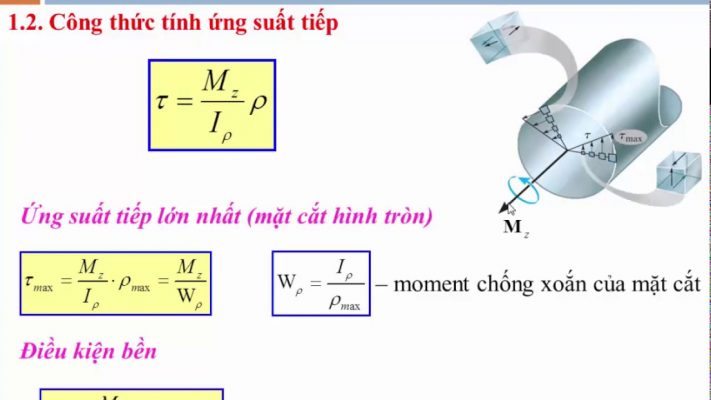
Công thức tính ứng suất ở một số ứng suất tiêu biểu

Công thức tính ứng suất cắt ra sao? Đây chắc hẳn là vấn đề được nhiều người quan tâm và tìm hiểu, nhất là những người làm việc trong lĩnh vực xây dựng, vật lý, cơ khí. Và để nắm được các công thức tính ứng xuất, mời các bạn cùng tham khảo bài viết dưới đây.

Khái niệm ứng suất cắt là gì?

Trước khi đi sâu vào tìm hiểu các công thức tính ứng suất chúng ta cũng cần phải biết ứng suất là gì? Theo đó, ứng suất là đại lượng biểu thị cho nội lực phát sinh trong vật thể biến dạng do chịu tác dụng của các nguyên nhân bên ngoài như tải trọng, sự thay đổi nhiệt độ,…

Phương trình ứng suất tổng quan: σ = FA

Trong đó:

• σ: ứng suất
• F: lực
• A: diện tích bề mặt

Ứng suất cắt và biến dạng mối hàn được sinh ra là do một số nguyên nhân 

Do nhiệt độ nung nóng và làm nguội không đều nên dẫn đến sự phân bố nhiệt độ trên các vật bị hàn và độ dãn nở của chúng cũng không đồng đều. Do đó, đã làm cho mối hàn và các vùng lân cận sinh ra ứng suất. Chính việc tạo ra ứng suất đã làm cho vật hàn bị biến dạng.

Do độ co ngót của kim loại lỏng ở vùng hàn khi kết tinh.

Khi đông đặc thể tích kim loại sẽ bị giảm vì vậy sẽ sinh ra ứng suất ở trong liên kết hàn. Đặc biệt, quá trình giảm thể tích của kim loại khi đông đặc còn được gọi là co ngót.

Do sự thay đổi của kim loại với các mối hàn và vùng lân cận quanh mối hàn.

Chịu sự ảnh hưởng của nhiệt nên phần kim loại mối hàn và các vùng lân cận sẽ thay đổi tổ chức, vì vậy sẽ tạo nên ứng suất trong vật hàn. Đặc biệt là các thép hợp kim và thép cacbon.

Một số loại ứng suất

Người ta có thể chia ứng suất thành một số tiêu chí sau:

• Ứng suất theo phạm vi tác động:  được chia làm 3 phạm vi
• Ứng suất theo hướng phân bố trong không gian: hướng 1 chiều theo chi tiết thanh; theo hướng 2 chiều bao gồm các chi tiết tấm và vỏ; theo hướng 3 chiều bao gồm các chi tiết có cả 3 chiều kích thước.
• Ứng suất theo hướng thời gian tồn tại: Ứng suất tức thời và ứng suất dư
• Ứng suất theo hướng tác động so với trục mối hàn: ứng suất trực được song song với trục mối hàn; ứng suất ngang thường vuông góc với trục mối hàn.

Các công thức tính ứng suất cắt

Công thức tính ứng suất pháp

Ứng suất pháp hay còn được gọi là ứng suất uốn (là kéo hoặc nén), có tác dụng vuông góc với mặt đối diện của phân tố ứng suất. Ứng suất kéo có xu hướng kéo phân tố, còn ứng suất nén có xu hướng nén.

Trong mặt cắt ngang của dầm, ứng suất uốn cực đại sẽ xuất hiện ở phần xa nhất tính từ trục trung hoà của mặt cắt.

Tại điểm đó, công thức tính ứng pháp lớn nhất như sau: = M.CL

Trong đó:

• M: độ lớn momen uốn tại mặt cắt
• I: mômen quán tính của mặt cắt ngang đối với trục trung hoà của nó
• c: khoảng cách từ trục trung hoà đến thớ ngoài cùng của mặt cắt ngang dầm.

Để thuận tiện cho việc thiết kế đưa ra thuật ngữ mômen chống uốn S=IC

= Công thức tính ứng suất uốn = MS

Vì I và c là các đặc trưng của hình học mặt cắt ngang dầm nên S cũng vậy. Khi đó, trong thiết kế thường xác định ứng suất d và mômen uốn đã biết, giải được S=Md

= Đây chính là kết quả này của giá trị yêu cầu mômen chống uốn; từ đó những kích thước yêu cầu mặt cắt ngang của dầm có thể được xác định.

Công thức tính ứng suất cắt

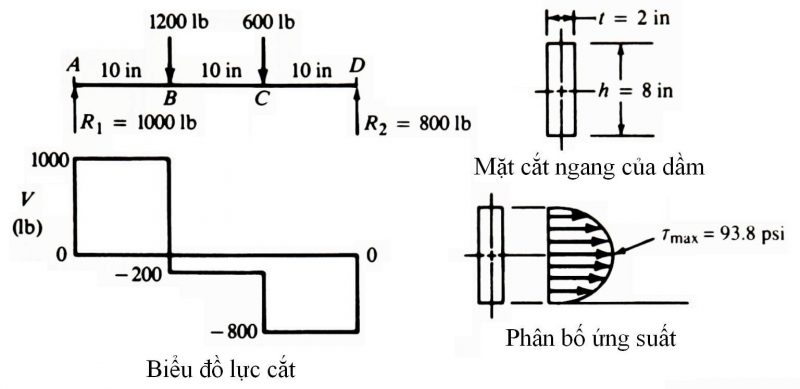
Khi một dầm đỡ tải trọng, trục đặt nằm ngang sẽ chịu lực cắt (V). Trong tính toán dầm, sẽ tính sự biến đổi của lực cắt trên toàn bộ chiều dài của dầm và vẽ biểu đồ lực cắt. Sau đó tính ứng suất cắt từ.

Ứng suất cắt đứng trong dầm: = VQI.t (3-16)

Trong đó:

• I: momen quán tính thẳng góc của mặt cắt ngang của dầm
• t: chiều dày của mặt cắt tại vị trí tính ứng suất
• Q: là momen cấp 1, đối với trục trung hoà của diện tích phần mặt cắt ngang nằm về một phía đường ngang với điểm tính ứng suất.

Để tính giá trị của Q, ta dùng công thức sau: Q = AP.y

Trong đó:

• AP: diện tích mặt cắt bên trên điểm tính ứng suất
• y: khoảng cách từ đường trung hoà của mặt cắt đến trọng tâm của diện tích

Công thức tính ứng xuất xoắn

Khi momen xoắn được đặt lên chi tiết, nó sẽ có xu hướng biến dạng do vặn, bởi một phần của chi tiết bị xoay kéo theo các phần khác nữa.

Sự vặn như vậy sẽ gây ra ứng suất xoắn trong chi tiết với một phân tố nhỏ. Bản chất của ứng suất này giống với ứng suất cắt trực tiếp. Tuy nhiên khi bị xoắn, ứng suất không phân bố đồng đều trên mặt cắt ngang.

Khi chịu momen xoắn, mặt ngoài của trục tròn đặc chịu biến dạng trượt lớn nhất và vì vậy ứng suất xoắn là lớn nhất.

Giá trị lớn nhất của ứng suất xoắn được xác định theo: max = T.cJ(1)

(c – bán kính mặt ngoài của trục J là mômen quán tính độc cực)

Khi muốn tính ứng suất xoắn tại một số điểm trong trục, thường sử dụng công thức chung như sau:  = T.rJ(2)

(r – bán kính từ tâm của trục đến điểm cần tính)

Để thuận tiện cho việc thiết kế và xác định mô đun chống xoắn ta có công thức tính mô đun chống xoắn: ZP = Jc(3)

= Từ (1), (2), (3) ta có công thức tính ứng suất xoắn lớn nhất là:

max = T ZP

Công thức tính ứng suất cắt trực tiếp

Ứng suất cắt trực tiếp sẽ xuất hiện khi lực tác dụng có xu hướng cắt qua chi tiết như kéo hoặc dao cắt hay khi chày và khuôn được dùng để đột một lỗ trên một tấm vật liệu nào đó.

Phương pháp tính ứng suất cắt trực tiếp tương tự giống với công thức tính ứng suất kéo vì khi đó lực tác dụng theo giả thiết được phân bố đều trên mặt cắt ngang chịu lực của chi tiết.

Công thức tính ứng suất cắt như sau:

Ứng suất cắt trực tiếp = lực cắt/ diện tích chịu cắt = FAS

Tên gọi chính xác hơn của ứng suất này là ứng suất cắt trung bình hay còn gọi là ứng suất phân bố đều trên diện tích cắt.

Công thức tính ứng suất gây lún

Dự tính độ lún ổn định của đất dựa trên kết quả của lý thuyết đàn hồi. Trong trường hợp đế móng vuông hoặc tròn, tải trọng phân bố đều thì độ lún của móng được tính bằng công thức sau:

S = pb (1- ²) E

Trong đó:

• p: ứng suất gây lún
• b: chiều rộng móng (đường kính móng tròn)
• ω: hệ số phụ thuộc hình dạng, kích thước đáy móng
• ωo:hệ số để tính độ lún tại tâm móng mềm
• ωc: hệ số để tính độ lún tại góc móng mềm
• ωm: hệ số để tính độ lún trung bình của móng mềm
• ωconst: hệ số để tính độ lún tại tâm móng cứng

Biểu diễn các ứng suất trên một phân tố ứng suất

Một mục tiêu quan trọng của phân tích ứng suất là xác định điểm trên chi tiết mang tải có mức ứng suất cao nhất.

Bạn sẽ phát triển khả năng xây dựng một phân tố ứng suất, một khối lập phương vô cùng nhỏ trong vùng ứng suất cao của chi tiết, và chỉ ra các véctơ biểu diễn cho những loại ứng suất tồn tại trên phân tố đó.

Sự định hướng của thành phần ứng suất có tính quyết định, và nó được hướng theo các trục đã xác định trên phân tố, thường gọi là x, y, và z.

Hình 3-5 chỉ ra 3 ví dụ của các phân tố ứng suất với ba loại ứng suất cơ bản là: kéo, nén và tiếp. Cả dạng khối lập phương hoàn chỉnh và dạng hình vuông đơn giản biểu diễn các phân tố ứng suất đều được chỉ ra.

Hình vuông là một mặt của khối lập phương trong mặt được chọn. Các hình vuông biểu diễn hình chiếu vuông góc các mặt của khối lập phương xuống mặt được chọn. Đầu tiên bạn cần lưu ý khi thể hiện khối lập phương và sau đó biểu diễn một phân tố ứng suất vuông chỉ ra ứng suất trên một mặt riêng mà bạn cần.

Trong một số trường hợp, với trạng thái ứng suất tổng quát hơn, có thể yêu cầu hai hoặc ba phân tố ứng suất vuông để mô tả một trạng thái ứng suất hoàn chỉnh.

Ứng suất kéo và nén, gọi là ứng suất pháp; tác dụng vuông góc với mặt đối diện của phân tố ứng suất. Ứng suất kéo có xu hướng kéo phân tố, trong khi ứng suất nén có xu hướng nén nó.

Ứng suất tiếp tạo ra bởi cắt trực tiếp, lực cắt trên dầm, hoặc xoắn.

Từ khóa:

• Công thức tính ứng suất xoắn
• Công thức tính ứng suất cắt
• Ký hiệu ứng suất
• Công thức tính ứng suất tương đương
• Ứng suất cho phép
• Ứng suất xoắn
• Ứng suất cắt

Nội dung liên quan:

• Cách Chọn Tiết Diện Dây Dẫn 3 Pha theo công suất
• Cách sửa máy lạnh bị nhỏ nước
• Cách sử dụng remote máy lạnh Samsung tiết kiệm điện